Pre-test'(x)

Hey, MrSiwWy here for Monday's scribe! Now, all that we really did during class was write the pre-test, though Graeme, Mark and I all decided to rush through it and discuss it in our own group so that we could leave early to practice for the Literacy presentation in the afternoon. I know that it was my fault that we lost a few silly marks because of the fact that we rushed through everything on Monday, but since I really haphazardly rushed and finished way too early some of my solutions were flawed (and we ended up handing in my paper). Well, that's in the past, so on to the scribe. Now, usually a scribe for a pre-test class wouldn't really be that detailed, but I feel obligated to try and explain the solution process for each of the questions on the pre-test as well as I can. I'll accompany each with the corresponding slide, to show Mr. K's work (if that question was brought up in class) and to show the question itself.

1. What is dc/dx, where c is a constant?


Well, this is simply testing to see if you remember the constant rule for differentiation. Thus the answer is simply (b) which is 0. It might help if I reviewed with you the basic idea of each of the rules we have learned for differentiation, since the test is just about 12 hours away from now.
Constant Rule: The constant rule basically dictates that any function that is solely just a constant, such as f(x) = 4, or g(x) = 13, has a derivative that is 0, or f'(x) = 0 and g'(x) = 0.
Coefficient Rule: When differentiating a first-order function with a coefficient, such as f(x) = 2x, or g(x) = 215x, the derivative will simply be that coefficient. In the examples given, f(x) = 2x yields f'(x) = 2, while g(x) = 215x yields g'(x) = 215.
Sum/Difference Rule: When a function is composed of more than one term, then you can break that function up into it's constituent parts and differentiate each part separately. Examples include f(x) = 388x + 6, or g(x) = 56x² - 21x, where f'(x) = 388 + 0 = 388, or g'(x) = 102x - 21.
Power Rule: For any function where x is raised to an exponent n, or f(x) = xⁿ, the derivative of that function will be x raised to the exponent (n-1) all multiplied by n, or f'(x) = nx^n-1.
Product Rule: For any function that is composed of two functions being multiplied together, the derivative is not the derivative of their product, nor is it the product of their respective derivatives. To find the derivative of a product, the derivative will always be given by h'(x) = f(x)g'(x) + g(x)f'(x), assuming h(x) = f(x)g(x). It's basically the derivative of the first function multiplied by the other function, then add on the derivative of the second function multiplied by the first function.
Quotient Rule: To find the derivative of a quotient, all you have to do is recall the quotient rule song! Assuming that h(x) = f(x) / g(x) then h'(x) = [g'(x)f(x) - f'(x)g(x)]/g²(x). Here's the song in case you forgot: "High de low minus low dehigh, all over low low"
Chain Rule: This must be used whenever a function is actually buried deep inside another function. This can be given by h(x) = f(g(x)), such as h(x) = (2x² + 3x)³. First you must find what g(x) is, or what the inner function is, then it should be easy to determine what is the outer function. The derivative of any composition of functions (when a function has another function inside of it) is given by h'(x) = g'(x)f'(g(x)). In the given example, the derivative would be h'(x) = (4x + 3)[3(2x² + 3x)²], or (12x + 9)(2x² + 3x)² since g(x) = 2x² + 3x and f(x) = x³.

2. What is dxⁿ/dx?


Again, this is just testing the knowledge of a rudimentary rule given above.

3. Given f(x) = √(1-x²) find and simplify f'(x).


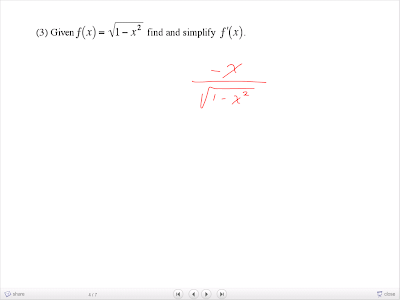
Well, this is basically just applying the rules of differentiating I reviewed above in a very straight forward manner. You must be able to recognize that you must use the chain rule with the inner function g(x) = 1 - x², while the outer function f(x) = √x. Then the derivative becomes f'(x) = -2x / 2 √(1-x²), which simplifies to f'(x) = -x / √(1-x²).

4. Find the equation of the line tangent to the graph of 8xy² = (x + y)⁴ at the point (1/2, 1/2).


This was a rather tricky question, but I remember first determining how I forgot to take the derivative of x + y as 1 + dy/dx, instead of just dy/dx, and I also forgot to distribute the 8 through the left side and didn't read the question and gave him only a slope for an answer. I really need to take my time answering these questions =/. Well anyways...

The solution is shown above, but the main idea behind solving this question is just realizing that you must differentiate the equation implicitly, since y might represent any one of a variety of possible functions. If you can see that you must differentiate implicitly, it's pretty just grunt work applying the above rules and keeping in mind the fact that any time you differentiate the variable y, you must use the chain rule since it has some unknown buried inside of it, meaning that that term must be multiplied by y'. In the work you can see this being done. Say a function x + y = 4 was to be differentiated, then afterwards it would transform into 1 + 1y' = 0, or y' = -1.

Don't forget, as I did, that the question is asking for the equation to the tangent line at (1/2, 1/2), not just the slope of that tangent line. So, once you can solve for y' as shown above through implicit differentiation, you can use the point given (1/2, 1/2) to find the equation of the tangent line, thus completing the question.

5. (a) If f(x) = √(x² + 9), use the limit definition of the derivative to find f'(0). You must show all work and use the limit definition properly to receive any credit.


The work for this question was once again fully shown by Mr. K, but the key to this question is realizing that it's asking for the derivative at a point, and not the derivative function of f(x). Using this knowledge, we can apply the limit definition at f(0) instead of f(x), and f(0+h) instead of at f(x+h). What Mr. K did with his work was that he determined what f(0) was by simply plugging 0 into x inside f(x), and then determined what f(0+h) would be by plugging in (0 + h) into f(x). He did this so that he could use the values he arrived at in these initial steps, and simply apply them to the limit definition as shown near the bottom of the slide.

5 (b) If g(x) = x2 - 3x + 4, use the definition of the derivative to find an equation or formula for the derivative of x. Again no credit will be awarded unless you demonstrate competent use of the limit definition and show all your work.


Once again you can see the solution to this question in the slide above. What you had to realize to solve this question is that you have to know what g(x+h) will be when expanded, as Mr. K has shown at the top portion of the slide. Once this is known, you must plug it into the fundamental limit definition of the derivative and things should start to cancel quickly and elegantly. In the final steps of the solution, once you plug in 0 into h, then the lim part goes away and any term with an h in it leaves along with it. Thus leaving 2x - 3, which gives the derivative of g(x), or rather gives g'(x).

Well that's it for my scribe post, I think that this might be one of my shortest scribe posts since way back in grade 12 pre-cal ^^. Too bad I wasn't present for the entire class, but I guess I tried to cover everything to the best of my ability since I was only present for maybe 20 minutes. Don't forgot to study tonight folks, since the test is tomorrow. I wish everyone the best of luck!
Oh yes, almost forgot, the next scribe will be: John D.