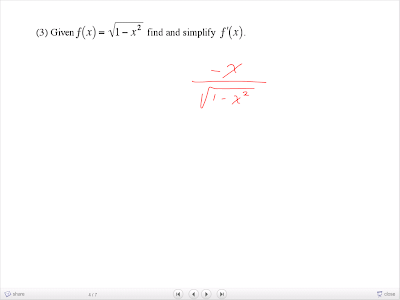So Long ...

We had our graduation exercises today. A gentle push into the world for all of you. I hope you're leaving with the keys to your future in your hand.

I'm so glad we've had this time together,

Just to have a laugh or learn some math,

Seems we've just got started and before you know it,

Comes the time we have to say, "So Long!"

So long everybody! Watch this space in the fall for pointers to new blogs for each of my classes.

Farewell, Auf Wiedersehen, Adieu, and all those good bye things. ;-)

Student Voices Episode 4: Justice, Lawrence, and Richard

First an update on this podcast: While we have received few comments on this or any of our class blogs the number of times the audio files have been downloaded is remarkable ...

Episode 1: Jessie 2440 downloads

Episode 2: Tim_MATH_y 1766 downloads

Episode 3: Chris, Craig, Graeme 1367 downloads

Thanks to all our listeners. We might get one more published during this school year but this may be the last until September. In any case feel free to let us know your thoughts about what you heard; every comment is appreciated.

In this episode of Student Voices Justice, Lawrence, and Richard talk about how they put together their Developing Expert Voices project and what they learned in the process: how they they best learn math, how it can best be taught, and many other incidental things like team work and organizational skills.

They have titled their project with one of my favourite reminders to all my students: Mathematics is the Science of Patterns. If you watch any of the video content they created you'll hear several "in jokes", listen for them. Without any further ado, here is the podcast. A copy of the poster they made for their work is below.


(Download File 12.2Mb, 25 min. 30 sec.)

Photo Credit: Shadow singer by flickr user EugeniusD80

Today's Slides: June 4

Here they are ...

| View | Upload your own

Introduction to Anti-Derivatives (sounds like some sort of medicine)

So, on the previous class, we were introduced to anti-derivatives..


At the beginning of the class, we were asked to find the derivatives of the above functions. Needless to say, we found it difficult... NOT. It's 2x for all functions. And then we were given the derivative, f ' (x) = x and were asked to find the parent function. We were quite stumped at first, but then managed to figure it out. We had to go back to a previous lesson since we were asked whether if given a constant and a function and if we had to find the derivative of the function, does the constant play a role? No, it doesn't. Anyway, we were asked to find the parent function of the derivative f ' (x) = x. If x is the derivative, then obviously the parent function is x². But the derivative of x² is 2x and the derivative we want is x. So we figured, we have to multiply 2x by 1/2 to get x. From that, we got the parent function, which is 1/2x². Mr. K then asked us, what about if I give you the derivative x²? What would be its parent function? We then thought about it. If x² is the derivative, obviously the parent function is x³. But the derivative of that function will give us 3x², which we don't want since we're given the derivative x². So we thought multiplying 3x² by 1/3 would give us x². We reckon that the parent function is 1/3x³. From that we came up with a rule for all power functions, which is:

f ' (x) = xⁿ -------> f (x) = xⁿ⁺¹/n+1 + C, where C is the constant. I'll explain later.


We then made anti-derivative rules for almost all derivative rules we remember. Mr. K said that the anti-derivative rules for the product and quotient rule are much more complicated and we won't be taking it until First Year University Calculus, so yeah.


Now this is where I explain the C part in the rule:

f ' (x) = xⁿ -------> f (x) = xⁿ⁺¹/n+1 + C, where C is the constant

We can't really find C not unless we're given a point in the graph. C is basically the y-intercept, but if we're just given the derivative and asked to solve for the parent function, all we can do is find the parent function and then + C, not unless we're given a point in the graph.

Then we were just given a practice problem, which was pretty straightforward.






The next scribe is etimz, or Ethan.

Today's Slides: May 23

Here they are ...

| View | Upload your own

BOB

Well, another test. This unit hasn't been so bad for me, I understand most of it. Hopefully I do well in the test. I do have a couple of problems with differentiating implicitly but it's nothing practice cannot solve. Otherwise, I'm good to go.

Good luck.

BOBBOBBOB!

What can I say? Well for one, this unit was simple the second time around =). I really think that I'm going to do well on this next test and yeah, hopefully I don't stumble on something that I haven't yet seen or tried to do. As always, the solution is practice! Hmm, I think the best place to start review would be to go through the past slides, and then see if I have any muddiest points.

This bob was short and straight to the point. I hope everyone remembers to bob and and and! Good luck on the test Wednesday I believe!

Today's Slides: May 16

Here they are ...

| View | Upload your own

Putting the pieces together

Today's lesson was about putting the pieces together, so to speak. Mr. K taught us how we should be able to come up with a graph of a function simply by using derivatives and critical points and whatnot.


This question was pretty straightforward. It just asks us to determine the critical points of the function, which means we have to find out where the derivative = 0. First we have to find the derivative of the certain function, as shown above, factor it if possible. However, don't make the mistake I did, which is state the CRITICAL NUMBERS instead of stating the CRITICAL POINTS. To find the critical points, just plug in the critical numbers at the parent function, and you should have it.



This is another straightforward question. Mr. K said that we should be able to solve these kinds of questions for 30-60 seconds. To find the relative max and min of an equation, we simply have to find out where the derivative of the parent function = 0. We then find the derivative of the parent function, as seen above, and then we use the first derivative test to find out if we have a maximum or a minimum. Then, we solve for the second derivative and use the second derivative test to find out again the maximum or a minimum of a function. An interesting tidbit: the second derivative function's main purpose is to find out the maximum or a minimum of a parent function. If we're only given the second derivative of a function, then yes, the 2nd derivative function is useful. Then Mr. K said, but what if we're given the parent function? Isn't that kind of a waste of time? The first derivative test already tells us the maximum or a minimum of a function, so why bother with the second derivative test? If it's main purpose is to find out the concavity of a parent function, then there we go.


For this question, we had to find out several things; intervals in which y is increasing or decreasing, the coordinates of any local extrema (minimum and maximum), intervals of concavity, inflection points, and the graph of the function. To find out where y is increasing or decreasing, we have to find out its derivative first and test the answers that we get. As you can see on the picture above, the critical numbers are x = 1 and 2. f is increasing where f ' is positive, and f is decreasing where f ' is negative. We then test it by using the number line test, and the

To find the coordinates of the local extrema, we use the first derivative test. From the number line test we did, we can see that we have a max at x = 1 and a min at x = 2. We then plug in those critical numbers on the parent function to find out the y coordinate of the maximum and the minimum points.

To find the intervals of concavity, we simply use the second derivative test. We find the derivative of the first derivative, which of course gives us the second derivative. We then find its critical point. We then use the number line test to find out where the parent function is concave up and concave down. From the solution above, we find out that the parent function is concave down from (-∞, 3/2) and concave up at (3/2, ∞). Therefore, we can say that we have a point of inflection at x = 3/2.


Well this is pretty straightforward. We just gather what we found out from the previous solutions and, shall I say, "put the pieces together." Then we sketch the graph. =)

That's it! We have a pre-test next class and a test the class after.

The next scribe is... *drum roll please*

haven't decided yet. lol

Today's Slides: May 14

Here they are ...

| View | Upload your own

Student Voices Episode 3: Chris, Craig, and Graeme

In this episode of Student Voices three Advanced Placement Calculus students, Chris, Craig, and Graeme, talk about a wiki assignment they did to prepare for the exam. Then the conversation transitions to a discussion of the many things they learned while doing their Developing Expert Voices project. It ends with a challenge, the result of which will be featured in a future podcast.

Let Chris, Craig, and Graeme know what you thought about the podcast by leaving a comment here on this post or on the mirror of this post on their class blog.

(Download File 31.8Mb, 26 min. 30 sec.)

The video mentioned near the end of the podcast is called Daft Hands. Here it is:

Photo Credit: Shadow singer by flickr user EugeniusD80

Scribe: Related Rates!

Introduction:

Hello, I'm known as Tim-Math-Y on our class blog and I will be the scribe for today's lessons! Today's class started with an image that introduced our content. The image was a combination of three that portrayed related rates with spheres, water ripples, and shadows. It was the precursor to the questions that we were to solve.

Key points to solving Related Rates questions:

• Find a way to relate all the variables within a given question
• Differentiate implicitly using chain rule, with respect to time

Content:

| View | Upload your own

Conclusion:

Well, I completed the scribe as soon as I could because it seemed that many people were missing today. I hope this helped!

Notice that most of these solutions include the following:

• A labelled diagram to help you visualize
• Listing given information, and finding information that will be required in the solution
  
• Differentiating implicitly using chain rule with respect to time
• A sentence answer including appropriate units

That sums it up folks! Thanks for reading =)

The Scribe for next class will be, John D. !

Today's Slides: May 12

Here they are ...

| View | Upload your own

The Post of TODAY!!

Today's Slides: May 8

Here they are ...

| View | Upload your own

More optimization problems

Hello everyone this is the scribe post for May 6, sorry it is late but I had to write the AP calc exam and I was not able to post it earlier. Well in Tuesday's class we only did one question, but there were two others for homework. The first question was about a man who was driving his car through the desert, and wanted to know at what distance he should drive through the desert and the paved road to get to the city B 5km south from city A. He can drive 15mph in the desert and 35mph on the paved road, he is 5 km east of city A. So the maximum distance the man could travel is 5km in the desert and 5km of pavement to get to city B (The diagram is on the slides). So that would be unrealistic, so in order to get the minimum amount of time the car must cut time through the desert and pavement alike. So the pavement equation will become 5km subtract x, x the amount of distance that is going to be cut by driving through the desert. Then the amount of distance driving through the desert is found by a^2 + b^2 = c^2. Where a and b is 5-x. So c is (25+x^2)^.5 (square root is ^.5).

As you know Rate, Distance, and Time is all related. Time is Distance over rate. So the total time is (5-x)/35 + ((25+x^2)^.5)/15 =t(x). Solving for the derivative (solved on the slides) , t'(x) =
7x-3((25+x^2)^0.5)/105((25-x^2)^0.5). Now solving for the zero's you get 40x^2-225. So the roots are -15/2((10)^0.5) and 15/2((10)^0.5). We reject the negative value because its not possible in the context of the question. So the man should go and head for the point x = 15/2((10)^0.5), as that point is the minimum value of the First Derivative Function.

Remember to do the other two questions and the homework given in class, the next scribe is Ethan.

Today's Slides: May 6

Here they are ...

| View | Upload your own

Optimization problems

Today, we were doing optimization problems.
In order to describe how we are solving these problems, I will be using an example from the slide 5.
It is the open box question where you have to cut squares from the corners to maximize the volume of the box.

First step is to draw a picture of what you want to do. We are cutting squares from the corners and we label the square's side with x. We know that the side of the entire piece is 24 inches per side. Therefore the equation is (24-2x) for the space between the two corner squares you have to cut. Everything is a square so all sides are the same.

Next we know that the volume of the box is going to be V=L*W*H.
We know that the height(H) is x and each side (L & W） is the same and equal to (24-2x), so the equation is going to be
V(x)= （24-2x)*(24-2x)*x
which is
V(x)=((24-2x)^2) * x

Third step is to simplify the equation and you will get
V(x)=(4x^3) - (96x^2) + 576x.

We take the derivative of that to find the max.
V'(x) =(12x^2) - 192x + 576
V'(x) =12((x^2) - 16x + 48)

The derivative at the max is equal to zero.
So we let V'(x) = 0
0 = 12((x^2) - 16x + 48)
0 = ((x^2) - 16x + 48)
0 = (x - 4) (x - 12)
x = 4, 12
x can't equal to 12 because that would make the side of the box equal to zero.
Therefore x = 4.

The last step is to test it.
___+___4__-___12_____

4 by 4 squares should be cut out to maximize the volume of the box.


The next scribe is Dino.

Today's Slides: May 2

Here they are ...

| View | Upload your own

Optimization Problems

Hey everyone this is m@rk and i'm scribing for Wednesday's class. First of we took a quiz on visual calculus about what we've learned from the first and second derivative test. Second , Mr. K introduced a new topic called Optimization Problems. Optimization problems are problems that deal with either finding the maximum or minimum of the function in the problem.

Slide 1

First of all you need to do is draw a diagram to help you visualize the problem. Second, construct the constraint equation. The constraint equation is the equation is something that limits the problem. In this case it is 320=2L+2W. Third, find what you are trying to optimize and construct an optimization equation. In this case you are trying to maximize area, so you need to use the area formula A=LW. Fourth, you need to solve for one of the unknown variables on the constraint equation and then plug it in on the optimization equation. We choose to solve for L in this case and we plug it in on the optimization equation. Fifth, solve for the derivative of our new optimization equation. Sixth, solve for the roots of the derivative of our optimization equation. We found out that the root is located at W=80. Seventh, use the first derivative test and find out whether it is a maximum or a minimum. Lastly, answer the question in a complete sentence.

I'm not going to go over the other question since it is just almost the same problem but instead I'm going to give you an outline how to solve an optimization problem, so after digging up the apcalc blog here it is:

Step 1: Find what you are trying to maximize or minimize. This will be stated excplicitly (in the question).

Step 2: Write an equation for it. Use V = for volume and M = for material, A for area, etc. I must insist on using descriptive variables, because in optimization, if you are sloppy, you lose track of what's going on.

Step 3: Try to get the equation into a two variable form, so you can take the derivative.
- Step 3a: To do step 1, you will often have to create a second equation from additional information given in the problem. This may require ingenuity, but it should become natural.
- Step 3b: ISolate one of the two variables in the equation drawn in step 3a.
- Step 3c: In the original equation that you are trying to minimize or maximize, replace the variable you isolated in step 3b.

Step 4: Take the derivative of your two-variable equation.

Step 5: Set the derivative to 0, and solve for the value of the remaining variable.

Step 6: Plus the value of that variable into the first two equations to find all dimensions, including the final goal, such as the amount of material, cost, or volume.

NOTE: This is just an outline so follow it loosely. There is really no chronological way to answer this problems.

Thats it , the next scribe is haiyan.

Today's Slides: April 30

Here they are ...

| View | Upload your own

The Hills and Valleys of Calculus

Why hello there, it's Kristin_R here, one of the few non-AP students left in the calculus class.


Today in class we learned about the first and second derivative tests.

The first derivative test:

c is a critical point (meaning the inputs where the derivative is zero or undefined, which is a horizontal tangent line) somewhere over the interval (a,b).

If f'(x) > 0 over the interval (a,c) and f'(x) < 0 for all values of x in the interval (c, b), then that function has a maximum over that interval.

If f'(x) ,0 over the interval (a,c) and f'(x) . 0 over the interval (c,b), then that function has a minimum over that interval.

Here's an example...

f(x) = x^2-8x=4

therefore, f'(x) = 2x-8

If we let the derivative equal zero, the root is at x=4.

When we plug four back into the original function, we get a y-value of -12. .

This means that the root is at (4, -12).

- ----- -12 ------ - --------4-------- +

By the first derivative test, x=4 is a minimum because to the left of 4, f is decreasing , and to the right of four, f is increasing.


The second derivative test:

When the parent function is concave up (valley), f'' is postive.

When the parent function is concave down (hill), f'' is negative.

When f' has a root, the parent function has a point of inflection, which is where the function changes concavity.

So, the first derivative test shows where the function is increasing or decreasing, as well as maximum or minimum extrema.

The second derivative test shows us the concavity of the graph.

"Just finding a root of your second derivative is not enough! You have to check your intervals!"

Just a quick little note - in grade eleven, you should have been taught about how to graph certain expontential functions. Remember that the degree of the given function is the same amount of possible roots in the graph.

So, thats it, thats the whole ball of wax...y'all dig?

Homework is up to and including page 64 in the white and orange book, as well as up to and including page 42 in the blue book.

The scribe for next class is....John. D!

The late Thursday scribe.

Yes me again. There actually isn't a lot of information to include on this scribe.

Due to the fact, Mr. K thought it was a lot of information to absorb for the past few classes.

So we....

basically reviewed Tuesday's class.

We got into groups, did the second slide question.

And critical numbers of f, are when f' and f'' are equal to zero.

Next scribe... Kristen.

Sorry it's so short...

The Last Tuesday Scribe

Sorry it's so late. Kept forgetting and procrastinating. Yes, it was supposed to be me... but, I wasn't even participating during the class, because of APcalc in the corner of the room. But, I can at least explain the slides.

Slide 1, 2

Picture and the question.

Slide 3,4,5

Velocity is the change of distance over the change in time.

a. The average velocity, is the slope of the line, from the interval 0 to 4 of the given position function.

b. Velocity is zero when, the derivative of x(t) is equal to zero.

c. When the point is moving to the right (positive) meaning, the velocity is positive. (Derivative of x is positive)

d. Same thing as c, but moving left (negative)

e. When the derivative is equal to 3

f. Taking the derivative of the velocity function. Or the second derivative of the position function, called the acceleration function is equal to 3.

q. (Not sure why q, but okay) Draw what x(t) looks like. Red graph is the derivative of x(t)

Slide 6,7

The graph, and line test means, you are trying to find from the derivative, where there may be local minimums or maximums on the parent function.

So, when the derivative has values that crosses the x axis(zero) there is a local maximum or minimum. To determine whether it is a maximum or a minimum, on the left side of the zero, if it is a positive value then crosses the x-axis and then is negative, it is a local maximum. Vice versa, it is a local minimum.

Slide 8

The extreme value theorem, says, on a differentiated function, within a closed interval, there exists a maximum and minimum value on the parent function.

Slide 9 and 10 practice what we just learned.

That's it for that scribe. I'm onto Thursday's scribe now. Ciao.

Today's Slides: April 28

Here they are ...

| View | Upload your own

Student Voices Episode 2: Tim_MATH_y

In this episode Timothy came back to school on Friday afternoon to talk about his week attending the miniUniversity program at the University of Winnipeg. He talks about the differences he finds between teaching and learning at high school and university and describes learning in the university classroom using a thought provoking metaphor, listen for it. Also, we have a cameo appearance by two very special people at the very end.

Please feel free to leave Tim_MATH_y your comments here on this post.

(Download File 7.2Mb, 15 min. 3 sec.)

Photo Credit: Shadow singer by flickr user EugeniusD80

Today's Slides: April 24

Here they are ...

| View | Upload your own

Today's Slides: April 22

Here they are ...

| View | Upload your own

Application of Derivatives

On Friday, our class started talking about the application of derivatives. To start off, Mr. K showed us this slide:


Mr. K then asked us when was the car moving fastest. The class decided that the car was moving fastest during t2, because the slope of the tangent line was the steepest at that point. During the interval [t1,t2], it is clear that the car is speeding up during that interval because the slope of the tangent lines are getting steeper going from t1 to t2. The car is definitely slowing down on the interval [t2,t3] as we can see that the slope of the tangent lines are decreasing.



Now this was a tough graph to decipher. The AP Calculus students had no problem understanding this one, but to those of us who aren't taking AP, this was kind of difficult. I myself found it quite confusing at first, but after clarification, I understand it. Now, you have to find the derivative of f in this graph to find out where is f ' is positive. First we have to find out where the tangent lines in f are zero. Looking at the function f, we can clearly see that the tangent lines are zero in -2 and +2. This means that f ' will have roots at -2 and +2. Then, we look when the tangent lines of f are approaching zero. There are 2 instances in this graph. The first instance is from (-∞, -2]. The slope from that domain is increasing, since it's coming from a negative value to zero. But that still doesn't solve our problem since f ' is still negative at that point. Then, from (-2, 2) in f, we can see that the slope is increasing until (0,0) and it starts to decrease until it reaches (2,3), where it becomes zero. At this point, f ' is positive as the slopes of the tangent lines from (-2, -1) to (0,0) are increasing from zero and reaches its maximum at (0,0), and then it starts to decrease from (0,0) until it reaches (2,3) where the slope is zero. This then solves the first question which asks where is f ' positive, which is from (-2, o) to (2,0).

Now to find out where f '' is positive. From the graph, we can see that f is some kind of a cubic function, so we know that its derivative will be a quadratic function. Now, the derivative of a quadratic function is a straight line, so now we know that f '' is a straight line. Looking at the shape of f ' (say it is -2x²), it is definitely a negative quadratic function because it has a maximum, not a minimum. We then have to find out the derivative of f '' which is represented as -2x² (However, it IS NOT -2x², it's just a representation). Using the power rule, we can determine that the derivative of f ', which is f '', is -4x. From this we can see that the function is positive at quadrant 2.

The critical numbers (which is another term for the roots) of f are -2 and 2.


This is a little difficult...
For a), f is increasing wherever f ' is positive.
For b), f(0) is negative.

Well, that was all we talked about last class. Mr. K tried to squeeze in one more slide but we ran out of time.

The next scribe is Kristin.

Student Voices Podcast Episode 1: Jessie

I was talking to Jessie, one of my Applied Math students, earlier this week while helping her review over the lunch hour. I found her comments so compelling I asked her (and later her parents) if I could record and publish her comments so other students could hear what she had to say. I've long thought students need to hear from other students how they best learn to help them all learn.

This is the first in what I hope will be a series of podcasts called Student Voices. I'm hoping to have one of these short conversations with a student published each week. If you'd like to volunteer to be featured in one of these just let me know.

In this episode Jessie shares how she uses her class blog to learn and describes her personal "tipping point" from being confused to understanding Statistics very well. She also discusses the value of learning conversations and how sometimes being a "teacher" and sometimes a student helps her learn.

Please feel free to leave Jessie your comments here or on this post on her class blog.

(Download File 5.6Mb, 11 min. 40 sec.)

Photo Credit: Kids of conversation by flickr user Kris Hoet

Today's Slides: April 18

Here they are ...

| View | Upload your own

1's - BoB^2

Something that I found that I thought was cool was when Mr. K showed us of something "brilliant" where we added terms - like adding zero.
This unit I thought was funner than the first unit - Limits. When you get to cancel or reduce terms and create a whole new equation different from the beginning it creates a feeling of completion if it is the derivative of that equation. I feel that I need some more work towards this unit to fully understand it - overall I like this unit out of the two: Limits and Derivatives.

BOB

Almost forgot to put up my BOB before the test. Whew.

Anyway, I thought this unit was pretty fun and stuff. There are some things I still have to work on, which is knowing when to apply the product rule and stuff. Other than that I think I'm pretty much know what's going on. A good sleep and breakfast should do the trick, and a good review too.

Night.

BOB Between Periods

Well, as I sit here and watch the hockey game, I will take some time (during an intermission of course) to reflect upon our last unit:

DERIVATIVES

Now I have already learned the content of this unit, and applied it many a time in the AP Calculus class. This means that everything on the test should be fairly easy for myself, but then again, it is one of Mr. K.'s tests.
As I saw with the Pre-Test, small mistakes are easy to make. Forgetting to take the derivate of a constant, or the other side of an equation can result in a major headache.
I think a good sleep, a hearty breakfast, and a little extra concentration should do the trick.

Good luck to all on the test.

Remember the derivative rules as well as the limit definition of a derivative!

Pre-test'(x)

Hey, MrSiwWy here for Monday's scribe! Now, all that we really did during class was write the pre-test, though Graeme, Mark and I all decided to rush through it and discuss it in our own group so that we could leave early to practice for the Literacy presentation in the afternoon. I know that it was my fault that we lost a few silly marks because of the fact that we rushed through everything on Monday, but since I really haphazardly rushed and finished way too early some of my solutions were flawed (and we ended up handing in my paper). Well, that's in the past, so on to the scribe. Now, usually a scribe for a pre-test class wouldn't really be that detailed, but I feel obligated to try and explain the solution process for each of the questions on the pre-test as well as I can. I'll accompany each with the corresponding slide, to show Mr. K's work (if that question was brought up in class) and to show the question itself.

1. What is dc/dx, where c is a constant?


Well, this is simply testing to see if you remember the constant rule for differentiation. Thus the answer is simply (b) which is 0. It might help if I reviewed with you the basic idea of each of the rules we have learned for differentiation, since the test is just about 12 hours away from now.
Constant Rule: The constant rule basically dictates that any function that is solely just a constant, such as f(x) = 4, or g(x) = 13, has a derivative that is 0, or f'(x) = 0 and g'(x) = 0.
Coefficient Rule: When differentiating a first-order function with a coefficient, such as f(x) = 2x, or g(x) = 215x, the derivative will simply be that coefficient. In the examples given, f(x) = 2x yields f'(x) = 2, while g(x) = 215x yields g'(x) = 215.
Sum/Difference Rule: When a function is composed of more than one term, then you can break that function up into it's constituent parts and differentiate each part separately. Examples include f(x) = 388x + 6, or g(x) = 56x² - 21x, where f'(x) = 388 + 0 = 388, or g'(x) = 102x - 21.
Power Rule: For any function where x is raised to an exponent n, or f(x) = xⁿ, the derivative of that function will be x raised to the exponent (n-1) all multiplied by n, or f'(x) = nx^n-1.
Product Rule: For any function that is composed of two functions being multiplied together, the derivative is not the derivative of their product, nor is it the product of their respective derivatives. To find the derivative of a product, the derivative will always be given by h'(x) = f(x)g'(x) + g(x)f'(x), assuming h(x) = f(x)g(x). It's basically the derivative of the first function multiplied by the other function, then add on the derivative of the second function multiplied by the first function.
Quotient Rule: To find the derivative of a quotient, all you have to do is recall the quotient rule song! Assuming that h(x) = f(x) / g(x) then h'(x) = [g'(x)f(x) - f'(x)g(x)]/g²(x). Here's the song in case you forgot: "High de low minus low dehigh, all over low low"
Chain Rule: This must be used whenever a function is actually buried deep inside another function. This can be given by h(x) = f(g(x)), such as h(x) = (2x² + 3x)³. First you must find what g(x) is, or what the inner function is, then it should be easy to determine what is the outer function. The derivative of any composition of functions (when a function has another function inside of it) is given by h'(x) = g'(x)f'(g(x)). In the given example, the derivative would be h'(x) = (4x + 3)[3(2x² + 3x)²], or (12x + 9)(2x² + 3x)² since g(x) = 2x² + 3x and f(x) = x³.

2. What is dxⁿ/dx?


Again, this is just testing the knowledge of a rudimentary rule given above.

3. Given f(x) = √(1-x²) find and simplify f'(x).


Well, this is basically just applying the rules of differentiating I reviewed above in a very straight forward manner. You must be able to recognize that you must use the chain rule with the inner function g(x) = 1 - x², while the outer function f(x) = √x. Then the derivative becomes f'(x) = -2x / 2 √(1-x²), which simplifies to f'(x) = -x / √(1-x²).

4. Find the equation of the line tangent to the graph of 8xy² = (x + y)⁴ at the point (1/2, 1/2).


This was a rather tricky question, but I remember first determining how I forgot to take the derivative of x + y as 1 + dy/dx, instead of just dy/dx, and I also forgot to distribute the 8 through the left side and didn't read the question and gave him only a slope for an answer. I really need to take my time answering these questions =/. Well anyways...

The solution is shown above, but the main idea behind solving this question is just realizing that you must differentiate the equation implicitly, since y might represent any one of a variety of possible functions. If you can see that you must differentiate implicitly, it's pretty just grunt work applying the above rules and keeping in mind the fact that any time you differentiate the variable y, you must use the chain rule since it has some unknown buried inside of it, meaning that that term must be multiplied by y'. In the work you can see this being done. Say a function x + y = 4 was to be differentiated, then afterwards it would transform into 1 + 1y' = 0, or y' = -1.

Don't forget, as I did, that the question is asking for the equation to the tangent line at (1/2, 1/2), not just the slope of that tangent line. So, once you can solve for y' as shown above through implicit differentiation, you can use the point given (1/2, 1/2) to find the equation of the tangent line, thus completing the question.

5. (a) If f(x) = √(x² + 9), use the limit definition of the derivative to find f'(0). You must show all work and use the limit definition properly to receive any credit.


The work for this question was once again fully shown by Mr. K, but the key to this question is realizing that it's asking for the derivative at a point, and not the derivative function of f(x). Using this knowledge, we can apply the limit definition at f(0) instead of f(x), and f(0+h) instead of at f(x+h). What Mr. K did with his work was that he determined what f(0) was by simply plugging 0 into x inside f(x), and then determined what f(0+h) would be by plugging in (0 + h) into f(x). He did this so that he could use the values he arrived at in these initial steps, and simply apply them to the limit definition as shown near the bottom of the slide.

5 (b) If g(x) = x2 - 3x + 4, use the definition of the derivative to find an equation or formula for the derivative of x. Again no credit will be awarded unless you demonstrate competent use of the limit definition and show all your work.


Once again you can see the solution to this question in the slide above. What you had to realize to solve this question is that you have to know what g(x+h) will be when expanded, as Mr. K has shown at the top portion of the slide. Once this is known, you must plug it into the fundamental limit definition of the derivative and things should start to cancel quickly and elegantly. In the final steps of the solution, once you plug in 0 into h, then the lim part goes away and any term with an h in it leaves along with it. Thus leaving 2x - 3, which gives the derivative of g(x), or rather gives g'(x).

Well that's it for my scribe post, I think that this might be one of my shortest scribe posts since way back in grade 12 pre-cal ^^. Too bad I wasn't present for the entire class, but I guess I tried to cover everything to the best of my ability since I was only present for maybe 20 minutes. Don't forgot to study tonight folks, since the test is tomorrow. I wish everyone the best of luck!
Oh yes, almost forgot, the next scribe will be: John D.

BOB ^ i2

MrSiwWy here for my second bob in intro to calculus. Oh wow, I just got home and I still have to scribe tonight =/ I don't expect to be faced with a terribly difficult test tomorrow, since we've already covered this unit in great depth in our AP calc class. Though, I must make sure to take my time this time and not to rush during any portion of the test, as I did on the pre-test (which cost me 2 rather easy marks). I'll probably explain that in more detail in my scribe post later tonight, but with that said, I don't think that there's anything I'm too worried about now. I usually make a longer bob than this, but I'll probably just integrate what I would usually say in my scribe post. Good luck on the test everyone ! Don't forget to practice those derivations!

BOB

Well, this unit about derivatives isn't too difficult considering that i learned this before. The only thing that i need to be careful on is working too fast for my own good. I usually make most of my mistakes on being too overconfident, but just to make sure I'll go over the orange and blue book tonight. Hopefully, i manage to get a good mark. Good luck everyone and study hard.

[B]logging [O]n [B]logging

Tomorrow is the test! Wow it's quite surprising how so many people have dropped this course throughout the minor portion of what has passed. Well, tomorrow is the test on Derivatives! It shouldn't be too difficult to be honest, especially for the AP Calc Students who have already learned this unit. Though I understand the most part of this unit, I know that I may still stumble somewhere, as questions are always different: there are always new wrinkles that you can run into.

Summary of Differentiation:

• Power Rule
• Product Rule
• F'(x) = f'(x) g(x) + f(x) g'(x)
  
• Quotient Rule
• Low D High, minus High D Low, All over Low Low (The SONG!)
• F'(x) = [ g(x) f'(x) - f(x) g'(x) ] / [ g(x) ]^2
• Chain Rule
• F'(x) = f'( g(x) ) g'(x)

Including these rules, remember to understand the Definition of a Derivative and how to find the derivative using this definition.

Good luck everyone!

Late Scribe x2 and Bob

Well I dropped the ball here, haven't really been paying too much attention to this particular blog of late. So by Murphy's law I was picked as scribe. Alright this isn't my best work I can tell you now, but this is how those two classes I have to scribe for go:

Day 1:

The point of this class was to come up with the equations of tangent lines and normal lines.
-Tangent lines are lines touch that touch the graph only once on a certain interval (the graph may wiggle and the tangent line can cross the graph at another point that does not matter)
-Normal lines are lines that are perpendicular to a tangent line.
-Recall that the first derivative of any funtion gives the slope of the graph at any point
-To find the equation of a tangent line at a point on a graph you need a couple things
-You need a point and you need slope
-You may use slope-intercept formula if you are given the y intercept y=mx+b
-But you'll probably be using point-slope formula (y-y1) = m(x - x1)
-So the general method to finding the formula of a tangent line to a point goes something like this:
-Find the derivative of your function
-Evaluate at your point
-Plug it into point-slope formula
and presto! There's your answer!

To find the equation of a normal line (a line that is perpendicular to a tangent line) there is only one more step. When you find the slope you just need to take the negative reciprocal of that and then plug it into our formula.

The last question we had that class asks us to find when the tangent line is horizontal. Well that is when the derivative equals zero. So you come up with the formula of the derivative then solve for the zeroes. Then you plug those x-co's back into the original function to find the points where the tangent line equals zero.

Day 2:

This class is a little more complicated.
-Mr.K started off with a talk about questions that the answers to were that just because we don't know for sure doesn't mean that something is or isn't there or happening.
-The shadow of the balcony, we would infer that there is a balcony casting that shadow, doesn't have to be, could be something that looks like a balcony.
-Then is that roof insulated? Well there is melted snow in places so we could assume no.
-Then do those people agree with one another? Through the story of Mr.K since their body language is all somewhat the same they probably are, but we don't know for sure.

-We then found the derivative of a semicircle.
-Mr.K showed us that we could define this function in other ways to get an infinite amount of other circle bits-and-pieces functions (see the slides)
-This was to show us that there could be many functions buried within another and that even though we don't know which one there may be we have to treat it as if there is another function within it and therefor when we differentiate we have to use the chain rule.
-One thing to notice about this is that the derivative might be in terms of y and x so you may need a set of coordinates to solve for the slope at a certain point instead of just an x-co.


Bob

I feel fairly confident for the upcoming test. No worries at all really. Schedule should die down a little so I wont' miss any more scribes or bobs!

G'night! (might edit this sometime to add some examples but I am *really* tired right now so sleep is a must... after bio...)

Today's Slides: April 14

Here they are ...

| View | Upload your own

Today's Slides: April 10

Here they are ...

| View | Upload your own

Today's Slides: April 8

Here they are ...

| View | Upload your own